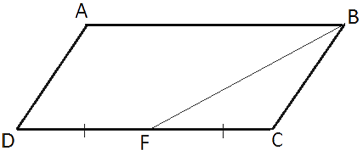Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
BC=CD/2=CF (по условию задачи)
Следовательно треугольник BCF -
равнобедренный.
По
свойству равнобедренного треугольника:
∠CFB=∠CBF
∠CFB=∠ABF (так как это
накрест-лежащие углы)
Получается, что ∠CBF=∠ABF
Следовательно, BF -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
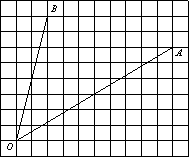Найдите тангенс угла AOB.
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-09-12 10:35:22) : АВ = CD = 14 см, ВС = AD = 27 см за властивостями параллелограмма Р ABCD = АВ + CD + ВС + AD Р ABCD = … Відповідь :