Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Рассмотрим треугольник AKD.
AK=AD (по условию задачи), следовательно данный треугольник
равнобедренный.
По
свойству равнобедренного треугольника ∠ADK=∠AKD
∠AKD=∠KDC (т.к. это
накрест-лежащие углы).
Получается, что ∠ADK=∠AKD=∠KDC.
Следовательно DK -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
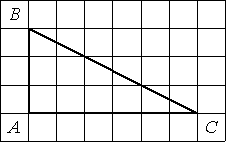Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-26 22:01:15) Администратор: Елена, потому, что ∠ADK=∠AKD, а ∠AKD=∠KDC.
(2014-05-26 18:30:51) Елена: почему ∠ADK=∠KDC.