
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ389 –Є–Ј 1087 |
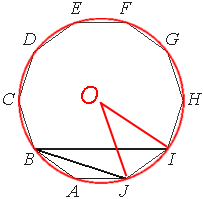
 ABCDEFGHIJ вАУ –њ—А–∞–≤–Є–ї—М–љ—Л–є –і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї IBJ. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
ABCDEFGHIJ вАУ –њ—А–∞–≤–Є–ї—М–љ—Л–є –і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї IBJ. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т–∞—А–Є–∞–љ—В 1 (–Я—А–µ–і–ї–Њ–ґ–Є–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –°–≤–µ—В–ї–∞–љ–∞)
 –Т–Њ–Ї—А—Г–≥ –ї—О–±–Њ–≥–Њ
–њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —Б–і–µ–ї–∞–µ–Љ —Н—В–Њ.
–Т–Њ–Ї—А—Г–≥ –ї—О–±–Њ–≥–Њ
–њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —Б–і–µ–ї–∞–µ–Љ —Н—В–Њ.
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ—В—А–µ–Ј–Ї–Є, –њ—А–Њ–≤–µ–і–µ–љ–љ—Л–µ –Є–Ј —Ж–µ–љ—В—А–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Ї —Г–≥–ї–∞–Љ –і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Њ–±—А–∞–Ј—Г—О—В —А–∞–≤–љ—Л–µ —Г–≥–ї—Л, —В–∞–Ї –Ї–∞–Ї —А–∞–Ј–±–Є–≤–∞—О—В –і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї –љ–∞ —А–∞–≤–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є.
–Ґ–∞–Ї–Њ–є —Г–≥–Њ–ї (–љ–∞–њ—А–Є–Љ–µ—А ∠IOJ) —А–∞–≤–µ–љ 360¬∞/10=36¬∞
∠IOJ —П–≤–ї—П–µ—В—Б—П
—Ж–µ–љ—В—А–∞–ї—М–љ—Л–Љ, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –≥—А–∞–і—Г—Б–љ–∞—П –Љ–µ—А–∞ –і—Г–≥–Є —В–Њ–ґ–µ —А–∞–≤–љ–∞ 36¬∞
∠IBJ —В–Њ–ґ–µ –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —Н—В—Г –ґ–µ –і—Г–≥—Г, –љ–Њ —П–≤–ї—П–µ—В—Б—П
–≤–њ–Є—Б–∞–љ–љ—Л–Љ, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ:
∠IBJ=36¬∞/2=18¬∞ (–њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ –≤–њ–Є—Б–∞–љ–љ–Њ–Љ —Г–≥–ї–µ)
–Ю—В–≤–µ—В: 18
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Ъ–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –≤ —В–Њ—З–Ї–∞—Е A –Є B –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –њ–Њ–і —Г–≥–ї–Њ–Љ 82¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABO. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ъ–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O –≤ —В–Њ—З–Ї–∞—Е A –Є B –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –њ–Њ–і —Г–≥–ї–Њ–Љ 82¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABO. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
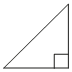 –Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –Њ–і–Є–љ –Є–Ј –Ї–∞—В–µ—В–Њ–≤ —А–∞–≤–µ–љ 7, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї, –њ—А–Є–ї–µ–ґ–∞—Й–Є–є –Ї –љ–µ–Љ—Г, —А–∞–≤–µ–љ 45¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –Њ–і–Є–љ –Є–Ј –Ї–∞—В–µ—В–Њ–≤ —А–∞–≤–µ–љ 7, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї, –њ—А–Є–ї–µ–ґ–∞—Й–Є–є –Ї –љ–µ–Љ—Г, —А–∞–≤–µ–љ 45¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
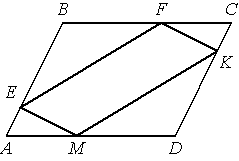 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D —В–Њ—З–Ї–Є E, F, K –Є –Ь –ї–µ–ґ–∞—В –љ–∞ –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞—Е, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ, –њ—А–Є—З—С–Љ BF = DM, BE = DK. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ EFKM вАФ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ –Р–Т–°D —В–Њ—З–Ї–Є E, F, K –Є –Ь –ї–µ–ґ–∞—В –љ–∞ –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞—Е, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ, –њ—А–Є—З—С–Љ BF = DM, BE = DK. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ EFKM вАФ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ.
 –Ъ–∞—В–µ—В—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л 20 –Є 15. –Э–∞–є–і–Є—В–µ —Б–Є–љ—Г—Б –љ–∞–Є–Љ–µ–љ—М—И–µ–≥–Њ —Г–≥–ї–∞ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Ъ–∞—В–µ—В—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л 20 –Є 15. –Э–∞–є–і–Є—В–µ —Б–Є–љ—Г—Б –љ–∞–Є–Љ–µ–љ—М—И–µ–≥–Њ —Г–≥–ї–∞ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Ъ–∞—В–µ—В—Л –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л
√

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: