Укажите номера верных утверждений.
1) Существует прямоугольник, который не является параллелограммом.
2) Треугольник с углами 40° , 70°, 70° — равнобедренный.
3) Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
Рассмотрим каждое утверждение:
1) "Существует прямоугольник, который не является параллелограммом", это утверждение неверно, т.к. любой
прямоугольник полностью удовлетворяет
определению параллелограмма.
2) "Треугольник с углами 40° , 70°, 70° — равнобедренный", это утверждение верно, по
свойству
равнобедренного треугольника.
3) "Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны". MA и MB -
касательные, тогда, по второму свойству касательной, это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
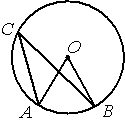Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
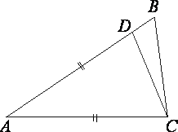Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
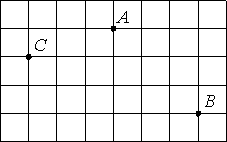На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол IBJ. Ответ дайте в градусах.
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: