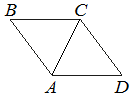
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Рассмотрим треугольник ABC.
AB=BC (по определению ромба).
Следовательно, треугольник ABC -
равнобедренный.
∠CAB=∠ACB (по свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ACB+∠ABC
180°=∠ACB+∠ACB+72°
180°-72°=2*∠ACB
108°=2*∠ACB
∠ACB=54°
Рассмотрим треугольники ABC и ADC:
1) AB=BC=CD=DA (по определению ромба).
2) AC - общая сторона.
Тогда по 3-му признаку данные треугольники равны.
Следовательно:
∠ACD=∠ACB=54°
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
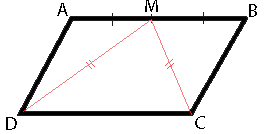В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
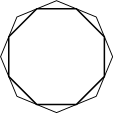Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: