Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
BC||AD (по
определению параллелограмма)
∠BAE=∠EAD (т.к. AE -
биссектриса)
∠EAD=∠BEA (т.к. это
накрест-лежащие углы)
Следовательно, ∠BAE=∠BEA
Получается, что треугольник ABE -
равнобедренный (по
свойству), и AB=BE (по
определению равнобедренного треугольника).
Аналогично с треугольником ECD:
∠CED=∠CDE
EC=CD
Так как AB=CD (по
свойству параллелограмма), то получается, что AB=BE=EC=CD=26.
BC=BE+EC=26+26=52.
Ответ: 52
Поделитесь решением
Присоединяйтесь к нам...
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
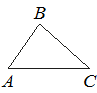В треугольнике ABC известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
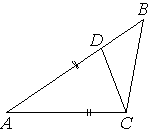Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: