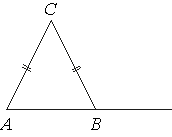
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
∠CBA - является
смежным внешнему углу, следовательно, 180°=∠CBA+121°
∠CBA=180°-121°=59°
Так как AC=BC, то треугольник ABC -
равнобедренный.
Значит ∠CBA=∠CAB=59° (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠CBA+∠CAB+∠C
180°=59°+59°+∠C
∠C=62°
Ответ: 62
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Катеты прямоугольного треугольника равны 4√
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: