ОГЭ, Математика.
Геометрия: Задача №201D88

Задача №653 из 1087
Условие задачи:

В треугольнике ABC AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.

Решение задачи:

∠CBA - является смежным внешнему углу, следовательно, 180°=∠CBA+154°
∠CBA=180°-154°=26°
Так как AC=BC, то треугольник ABC - равнобедренный.
Значит ∠CBA=∠CAB=26° (по свойству равнобедренного треугольника)
По теореме о сумме углов треугольника:
180°=∠CBA+∠CAB+∠C
180°=26°+26°+∠C
∠C=128°
Ответ: 128

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №A77323

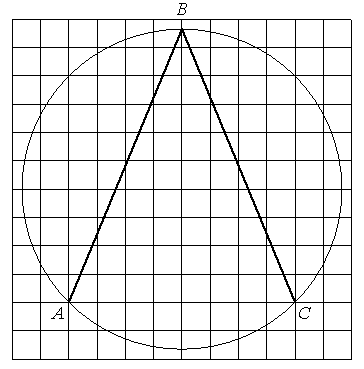Найдите угол ABC. Ответ дайте в градусах.

Задача №0C7DF1

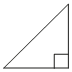В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.

Задача №7ABB40

Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.