Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=34.
BC||AD (по
определению параллелограмма)
∠BAE=∠EAD (т.к. AE -
биссектриса)
∠EAD=∠BEA (т.к. это
накрест-лежащие углы)
Следовательно, ∠BAE=∠BEA
Получается, что треугольник ABE -
равнобедренный (по
свойству), и AB=BE (по
определению равнобедренного треугольника).
Аналогично с треугольником ECD:
∠CED=∠CDE
EC=CD
Так как AB=CD (по
свойству параллелограмма), то получается, что AB=BE=EC=CD.
Значит, BE=BC/2=34/2=17.
AB=BE=17
Ответ: AB=17
Поделитесь решением
Присоединяйтесь к нам...
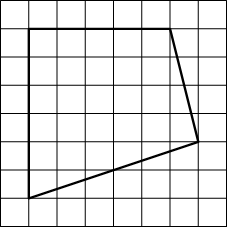Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
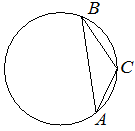
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
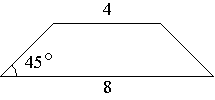В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
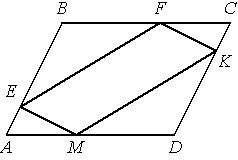В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В треугольнике ABC угол C равен 120°, AB=22√3. Найдите радиус окружности, описанной около этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: