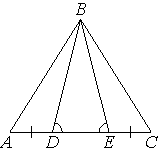
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АEB и BDC тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи /BED=/EDB, следовательно треугольник BDE - равнобедренный (по
свойству). По
определению равнобедренного треугольника BE=BD.
Смежные углы для углов /BED и /EDB тоже равны, /BDA=/BEC.
2) Рассмотрим треугольники ABD и CBE.
AD=EC (по условию),
BE=BD (согласно п.1),
/BDA=/BEC (из п.1),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
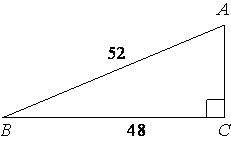Найдите площадь треугольника, изображённого на рисунке.
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: