В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 80°. Найдите величину угла ODC.
Рассмотрим треугольник AOB. Этот треугольник
равнобедренный, т.к. ОA и ОB - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/ABO=80°.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=80°
Ответ: /ODC=80°.
Поделитесь решением
Присоединяйтесь к нам...
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
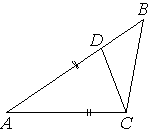Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=19° и ∠ACB=160°. Найдите угол DCB. Ответ дайте в градусах.
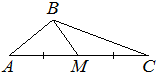В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
Какой угол (в градусах) описывает часовая стрелка за 2 минуты?
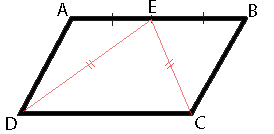В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: