
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ260 –Є–Ј 1087 |
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –Њ—Б–љ–Њ–≤–∞–љ–Є–µ AD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ –Њ—Б–љ–Њ–≤–∞–љ–Є—П –Т–° –Є –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ—Л CD. –£–≥–Њ–ї ADC —А–∞–≤–µ–љ 60¬∞, —Б—В–Њ—А–Њ–љ–∞ AB —А–∞–≤–љ–∞ 6. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –Њ—Б–љ–Њ–≤–∞–љ–Є–µ AD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ –Њ—Б–љ–Њ–≤–∞–љ–Є—П –Т–° –Є –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ—Л CD. –£–≥–Њ–ї ADC —А–∞–≤–µ–љ 60¬∞, —Б—В–Њ—А–Њ–љ–∞ AB —А–∞–≤–љ–∞ 6. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
–Т–∞—А–Є–∞–љ—В 1 (–њ—А–µ–і–ї–Њ–ґ–Є–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Т—Б–µ–≤–Њ–ї–Њ–і)
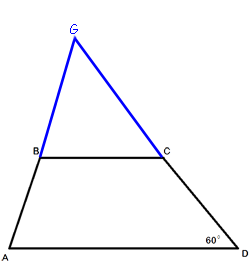 –Я—А–Њ–і–Њ–ї–ґ–Є–Љ —Б—В–Њ—А–Њ–љ—Л AB –Є CD –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ G.
–Я—А–Њ–і–Њ–ї–ґ–Є–Љ —Б—В–Њ—А–Њ–љ—Л AB –Є CD –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ G.
BC || AD (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —В—А–∞–њ–µ—Ж–Є–Є).
AD –≤–і–≤–Њ–µ –±–Њ–ї—М—И–µ BC (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є), —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ:
BC -
—Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ AGD.
–Ґ–Њ–≥–і–∞, CD=CG=AD/2 (–њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є).
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ AD=DG, —В.–µ. —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AGD -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, ∠AGD=∠GAD=x (
—Б–≤–Њ–є—Б—В–≤–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞)
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞:
180¬∞=∠AGD+∠GAD+∠ADG
180°=x+x+60°
120°=2x
x=60¬∞, —В.–µ. –≤—Б–µ —Г–≥–ї—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ADG —А–∞–≤–љ—Л 60¬∞, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –і–∞–љ–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї
—А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AG=DG, —В–Њ–≥–і–∞ –Є AB=CD, —В.–µ.
—В—А–∞–њ–µ—Ж–Є—П ABCD
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–∞—П.
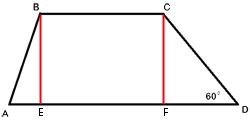 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Л BE –Є CF –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Л BE –Є CF –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
AD=AE+EF+FD, EF=BC=6 (—В–∞–Ї –Ї–∞–Ї BCFE -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї), AE=FD=y (—В–∞–Ї –Ї–∞–Ї —В—А–∞–њ–µ—Ж–Є—П —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–∞—П).
12=y+6+y
y=3
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞ CD2=CF2+FD2
62=CF2+32
CF2=27, CF=3√
SABCD=((BC+AD)/2)*CF=((6+12)/2)*3√
SABCD=27√
–Ю—В–≤–µ—В: SABCD=27√
 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Л BE –Є CF –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Л BE –Є CF –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –¶–µ–љ—В—А –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –ї–µ–ґ–Є—В –љ–∞ –≤—Л—Б–Њ—В–µ, –њ—А–Њ–≤–µ–і—С–љ–љ–Њ–є –Ї –Њ—Б–љ–Њ–≤–∞–љ–Є—О —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
2) –Ъ–≤–∞–і—А–∞—В —П–≤–ї—П–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ.
3) –°—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ –ї—О–±–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞
180°.
 –С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=5, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 5.
–С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –µ—Б–ї–Є BC=5, –∞ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є K –і–Њ —Б—В–Њ—А–Њ–љ—Л AB —А–∞–≤–љ–Њ 5.
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AD=3, BC=1, –∞ –µ—С –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 12. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AD=3, BC=1, –∞ –µ—С –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 12. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
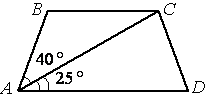 –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М –Р–° –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є –Р–Т —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 25¬∞ –Є 40¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї—М –Р–° –Њ–±—А–∞–Ј—Г–µ—В —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ AD –Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–Њ–є –Р–Т —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 25¬∞ –Є 40¬∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AB=CD, ∠BDA=62¬∞ –Є ∠BDC=42¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AB=CD, ∠BDA=62¬∞ –Є ∠BDC=42¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.


–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-03-15 18:10:35) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т—Б–µ–≤–Њ–ї–Њ–і, —Б–Њ–≥–ї–∞—Б–µ–љ —Б –Т–∞–Љ–Є!
(2015-03-15 17:49:50) –Т—Б–µ–≤–Њ–ї–Њ–і: –£–≤–∞–ґ–∞–µ–Љ—Л–є –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А! –°–њ–∞—Б–Є–±–Њ –Т–∞–Љ –Ј–∞ –≤–µ–і–µ–љ–Є–µ —В–∞–Ї–Њ–≥–Њ –њ–Њ–ї–µ–Ј–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞. –°–њ–∞—Б–Є–±–Њ –Є –Ј–∞ –Њ—Ж–µ–љ–Ї—Г –Љ–Њ–µ–≥–Њ –і–Њ–њ–Њ–ї–љ–µ–љ–Є—П. –Э–∞ –Љ–Њ–є –≤–Ј–≥–ї—П–і, —З–µ–Љ –±–Њ–ї—М—И–µ —А–∞–Ј–љ—Л—Е –њ–Њ–і—Е–Њ–і–Њ–≤, —В–µ–Љ —И–Є—А–µ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ —Г –≤—Б–µ—Е –Є–љ—В–µ—А–µ—Б—Г—О—Й–Є—Е—Б—П.
(2015-03-14 22:00:48) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т—Б–µ–≤–Њ–ї–Њ–і, –Њ—З–µ–љ—М –љ–µ–њ–ї–Њ—Е–Њ–є –≤–∞—А–Є–∞–љ—В! –Т —Б–Ї–Њ—А–Њ–Љ –≤—А–µ–Љ–µ–љ–Є –Њ–њ—Г–±–ї–Є–Ї—Г—О –њ–Њ –Т–∞—И–Є–Љ –Є–Љ–µ–љ–µ–Љ.
(2015-03-14 18:21:37) –Т—Б–µ–≤–Њ–ї–Њ–і: –Я—А–µ–і–ї–∞–≥–∞—О —З—Г—В—М –і—А—Г–≥–Њ–є –≤–∞—А–Є–∞–љ—В –њ–µ—А–≤–Њ–є –њ–Њ–ї–Њ–≤–Є–љ—Л —А–µ—И–µ–љ–Є—П. –Я—А–Њ–і–Њ–ї–ґ–Є–Љ —Б—В–Њ—А–Њ–љ—Л AB –Є CD –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ G. –Ф–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ADG –Њ—Б–љ–Њ–≤–∞–љ–Є–µ —В—А–∞–њ–µ—Ж–Є–Є BC (BC=AD/2) –±—Г–і–µ—В —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–µ–є, –Ј–љ–∞—З–Є—В CD=CG=AD/2, –Њ—В—Б—О–і–∞ AD=DG, –∞ —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –љ–Є–Љ–Є 60 –≥—А–∞–і—Г—Б–Њ–≤, –Ј–љ–∞—З–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ADG —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–є, –∞ —В–Њ–≥–і–∞ —В—А–∞–њ–µ—Ж–Є—П —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–∞—П.