
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Рассмотрим каждое утверждение:
1) "Любой квадрат является ромбом", это утверждение верно, т.к.
квадрат удовлетворяет определению
ромба.
2) "Против равных сторон треугольника лежат равные углы", это утверждение верно (по свойству
равнобедренного и
равностороннего треугольников).
3) "Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности", это утверждение верно. Эта система (точка и окружность) имеет
ось симметрии - прямая проведенная через данную точку и центр окружности. Соответственно, если можно провести одну
касательную, то можно провести и вторую, симметричную первой.
Ответ: 1), 2) и 3)
Поделитесь решением
Присоединяйтесь к нам...
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
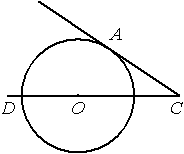 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
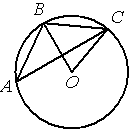 Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
 Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.


Комментарии: