Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Рассмотрим каждое утверждение:
1) "
Медиана
равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию", это утверждение верно, т.к. это
свойство
равнобедренного треугольника.
2) "Диагонали любого прямоугольника делят его на 4 равных треугольника", это утверждение неверно, т.к. у равных треугольников равны все стороны, а одна из сторон треугольников совпадает с одной из стороной прямоугольника. А соседние стороны прямоугольника могут быть не равны друг другу, тогда и стороны треугольников будут не равны, а значит и неравны сами треугольники.
3) "Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса", это утверждение верно, это становится очевидным, если провести радиус через эту точку.
Поделитесь решением
Присоединяйтесь к нам...
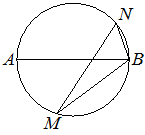На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
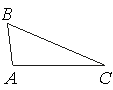В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 6:5. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Найдите угол ABC . Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: