
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ897 –Є–Ј 1087 |
 –Э–∞–є–і–Є—В–µ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є —Г–≥–ї—Л ABC –Є BCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 60¬∞ –Є 150¬∞, –∞ CD=33.
–Э–∞–є–і–Є—В–µ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є —Г–≥–ї—Л ABC –Є BCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 60¬∞ –Є 150¬∞, –∞ CD=33.
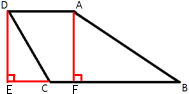 –Ф–Њ—З–µ—А—В–Є–Љ –Њ—В—А–µ–Ј–Ї–Є –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Ф–Њ—З–µ—А—В–Є–Љ –Њ—В—А–µ–Ј–Ї–Є –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
DE=AF, —В.–Ї. —Н—В–Њ
–≤—Л—Б–Њ—В—Л
—В—А–∞–њ–µ—Ж–Є–Є.
∠DCE=180¬∞-∠BCD=180¬∞-150¬∞=30¬∞ (—В.–Ї. —Н—В–Њ
—Б–Љ–µ–ґ–љ—Л–µ —Г–≥–ї—Л).
sin(∠DCE)=ED/CD (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О)
sin30¬∞=ED/CD (sin30¬∞=1/2 –њ–Њ
—В–∞–±–ї–Є—Ж–µ)
1/2=ED/33
ED=33*1/2=16,5
sin(∠ABF)=AF/AB (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О)
sin60°=ED/AB
AB=ED/sin60¬∞ (sin60¬∞=√3/2 –њ–Њ
—В–∞–±–ї–Є—Ж–µ)
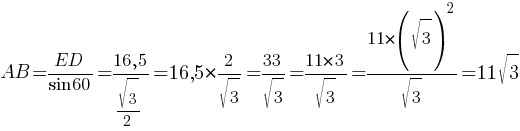
–Ю—В–≤–µ—В: 11√3
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–°—В–Њ—А–Њ–љ—Л AC, AB, BC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ—Л 3√
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 18√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 18√
 –Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC (–Р–Т=–Т–°) —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї MNK вАФ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
–Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC (–Р–Т=–Т–°) —В–Њ—З–Ї–Є M, N, K вАФ —Б–µ—А–µ–і–Є–љ—Л —Б—В–Њ—А–Њ–љ –Р–Т, –Т–°, –°–Р —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї MNK вАФ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, BC=5, AC=2.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, BC=5, AC=2.
–Э–∞–є–і–Є—В–µ tgB.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AL, —Г–≥–Њ–ї ALC —А–∞–≤–µ–љ 52¬∞, —Г–≥–Њ–ї ABC —А–∞–≤–µ–љ 13¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AL, —Г–≥–Њ–ї ALC —А–∞–≤–µ–љ 52¬∞, —Г–≥–Њ–ї ABC —А–∞–≤–µ–љ 13¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
| α | sinα | cosα | tgα | ctgα |
| 0° | 0 | 1 | 0 | --- |
| 30° | 1/2 | à |
√ |
√ |
| 45° | à |
√ |
1 | 1 |
| 60° | à |
1/2 | √ |
√ |
| 90° | 1 | 0 | --- | 0 |
| 120° | à |
-1/2 | -√ |
0 |
| 135° | à |
-√ |
-1 | -1 |
| 150° | 1/2 | -à |
-√ |
-√ |
| 180° | 0 | -1 | 0 | --- |
| 210° | -1/2 | -à |
√ |
√ |
| 225° | -à |
-√ |
1 | 1 |
| 240° | -à |
-1/2 | √ |
√ |
| 270° | -1 | 0 | --- | 0 |
| 300° | -à |
1/2 | -√ |
-√ |
| 315° | -à |
√ |
-1 | -1 |
| 330° | -1/2 | à |
-√ |
-√ |
| 360° | 1 | 0 | 0 | --- |
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: