Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
По
первому свойству равностороннего треугольника, все его углы равны 60°.
По
теореме синусов:
2R=a/sin60
a=2R*sin60 (найдем sin60 по таблице)
a=2*16*√3/2=16√3
По второму свойству равностороннего треугольника, высота равна:
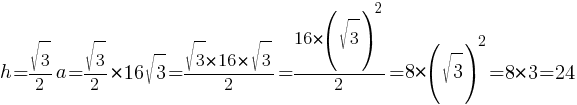
Ответ: 24
Поделитесь решением
Присоединяйтесь к нам...
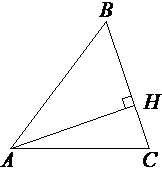В остроугольном треугольнике ABC высота AH равна 20√
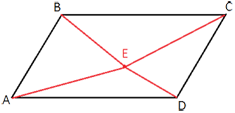Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
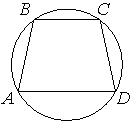Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
| α | sinα | cosα | tgα | ctgα |
| 0° | 0 | 1 | 0 | --- |
| 30° | 1/2 | √ |
√ |
√ |
| 45° | √ |
√ |
1 | 1 |
| 60° | √ |
1/2 | √ |
√ |
| 90° | 1 | 0 | --- | 0 |
| 120° | √ |
-1/2 | -√ |
0 |
| 135° | √ |
-√ |
-1 | -1 |
| 150° | 1/2 | -√ |
-√ |
-√ |
| 180° | 0 | -1 | 0 | --- |
| 210° | -1/2 | -√ |
√ |
√ |
| 225° | -√ |
-√ |
1 | 1 |
| 240° | -√ |
-1/2 | √ |
√ |
| 270° | -1 | 0 | --- | 0 |
| 300° | -√ |
1/2 | -√ |
-√ |
| 315° | -√ |
√ |
-1 | -1 |
| 330° | -1/2 | √ |
-√ |
-√ |
| 360° | 1 | 0 | 0 | --- |
Автор: Таська
Комментарии: