
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ739 –ł–∑ 1087 |
 –ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 18√
–ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 18√
–ě–Ī–ĺ–∑–Ĺ–į—á–ł–ľ:
a - –ł—Ā–ļ–ĺ–ľ—č–Ļ –ļ–į—ā–Ķ—ā
b - –≤—ā–ĺ—Ä–ĺ–Ļ –ļ–į—ā–Ķ—ā
c - –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–į
sin60¬į=√
sin60¬į=a/c=√
c=2a/√
–ü–ĺ
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ü–ł—Ą–į–≥–ĺ—Ä–į:
a2+b2=c2
a2+b2=(2a/√
a2+b2=4a2/3
3(a2+b2)=4a2
3a2+3b2=4a2
3b2=a2
b2=a2/3
b=a/√
–ė–∑ —É—Ā–Ľ–ĺ–≤–ł—Ź:
S—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į=ab/2=18√
a*(a/√
a2/√
a2=√
a2=36(√
a2=36
a=6
–ě—ā–≤–Ķ—ā: 6
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
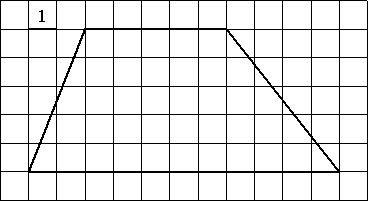 –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
 –í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AD=4, BC=3, –į –Ķ—Ď –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–į–≤–Ĺ–į 84. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł BCNM, –≥–ī–Ķ MN ‚ÄĒ —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AD=4, BC=3, –į –Ķ—Ď –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–į–≤–Ĺ–į 84. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł BCNM, –≥–ī–Ķ MN ‚ÄĒ —Ā—Ä–Ķ–ī–Ĺ—Ź—Ź –Ľ–ł–Ĺ–ł—Ź —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD.
 –Ę–ĺ—á–ļ–į O ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–į—ā —ā–ĺ—á–ļ–ł S, T –ł V —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —á—ā–ĺ OSTV ‚Äď —Ä–ĺ–ľ–Ī. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ OVT. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ę–ĺ—á–ļ–į O ‚Äď —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–į—ā —ā–ĺ—á–ļ–ł S, T –ł V —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —á—ā–ĺ OSTV ‚Äď —Ä–ĺ–ľ–Ī. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ OVT. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –ü—Ä—Ź–ľ–į—Ź, –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź–ľ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł
ABCD, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā –Ķ—Ď –Ī–ĺ–ļ–ĺ–≤—č–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CD –≤ —ā–ĺ—á–ļ–į—Ö E –ł F —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ĺ—ā—Ä–Ķ–∑–ļ–į EF, –Ķ—Ā–Ľ–ł AD=42, BC=14, CF:DF=4:3.
–ü—Ä—Ź–ľ–į—Ź, –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź–ľ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł
ABCD, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā –Ķ—Ď –Ī–ĺ–ļ–ĺ–≤—č–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CD –≤ —ā–ĺ—á–ļ–į—Ö E –ł F —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ĺ—ā—Ä–Ķ–∑–ļ–į EF, –Ķ—Ā–Ľ–ł AD=42, BC=14, CF:DF=4:3.
 –Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ BH, –Ķ—Ā–Ľ–ł PK=13.
–Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ BH, –Ķ—Ā–Ľ–ł PK=13.





–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: