
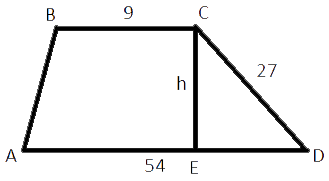
 Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту.
По
определению cos(/CDE)=ED/CD
√
ED=3*√
По
теореме Пифагора:
CD2=ED2+EC2
272=(3*√
729=9*65+EC2
EC2=144
EC=12 - это и есть высота
Sтрапеции=EC*(BC+AD)/2
Sтрапеции=12*(9+54)/2
Sтрапеции=6*63=378
Ответ: Sтрапеции=378
Поделитесь решением
Присоединяйтесь к нам...
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
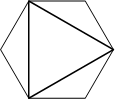 Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.





Комментарии: