
Катеты прямоугольного треугольника равны
√
 Т.к. треугольник
прямоугольный, мы можем применить
теорему Пифагора:
Т.к. треугольник
прямоугольный, мы можем применить
теорему Пифагора:
AB2=BC2+CA2
AB2=(√
AB2=15+1=16
AB=4
Наименьший угол лежит напротив наименьшей стороны (по
теореме о соотношении сторон и углов).
Тогда наименьший угол - /ABC (т.к. 1 < √
sin(/ABC)=AC/AB=1/4=0,25
Ответ: синус наименьшего угла равен 0,25.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
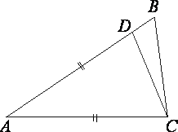 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?





Комментарии: