
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ293 –Η–Ζ 1087 |
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C –Ω―Ä―è–Φ–Ψ–Ι, BC=6, cosB=0,3. –ù–Α–Ι–¥–Η―²–Β AB.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C –Ω―Ä―è–Φ–Ψ–Ι, BC=6, cosB=0,3. –ù–Α–Ι–¥–Η―²–Β AB.
–ü–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é –Κ–Ψ―¹–Η–Ϋ―É―¹–Α cosB=BC/AB => AB=BC/cosB=6/0,3=20.
–û―²–≤–Β―²: AB=20.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ù–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Β –ê–Γ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ –≤―΄–±―Ä–Α–Ϋ―΄ ―²–Ψ―΅–Κ–Η D –Η E ―²–Α–Κ, ―΅―²–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Η AD –Η CE ―Ä–Α–≤–Ϋ―΄ (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –û–Κ–Α–Ζ–Α–Μ–Ψ―¹―¨, ―΅―²–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Η BD –Η BE ―²–Ψ–Ε–Β ―Ä–Α–≤–Ϋ―΄. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–£–Γ βÄî ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι.
–ù–Α ―¹―²–Ψ―Ä–Ψ–Ϋ–Β –ê–Γ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –ê–£–Γ –≤―΄–±―Ä–Α–Ϋ―΄ ―²–Ψ―΅–Κ–Η D –Η E ―²–Α–Κ, ―΅―²–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Η AD –Η CE ―Ä–Α–≤–Ϋ―΄ (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –û–Κ–Α–Ζ–Α–Μ–Ψ―¹―¨, ―΅―²–Ψ –Ψ―²―Ä–Β–Ζ–Κ–Η BD –Η BE ―²–Ψ–Ε–Β ―Ä–Α–≤–Ϋ―΄. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ –ê–£–Γ βÄî ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι.
 –Γ―²–Ψ―Ä–Ψ–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Ϋ–Α 6√3. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ –Κ–≤–Α–¥―Ä–Α―²–Α.
–Γ―²–Ψ―Ä–Ψ–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²–Α ―Ä–Α–≤–Ϋ–Α 6√3. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―ç―²–Ψ–≥–Ψ –Κ–≤–Α–¥―Ä–Α―²–Α.
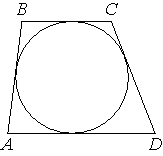 –Δ―Ä–Α–Ω–Β―Ü–Η―è ABCD ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ–Η AD –Η BC –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, AB=14, BC=13, CD=22. –ù–Α–Ι–¥–Η―²–Β AD.
–Δ―Ä–Α–Ω–Β―Ü–Η―è ABCD ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è–Φ–Η AD –Η BC –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, AB=14, BC=13, CD=22. –ù–Α–Ι–¥–Η―²–Β AD.
 –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD ―Ä–Α–≤–Ϋ–Α 5. –Δ–Ψ―΅–Κ–Α E βÄ™ ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AD. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η AECB.
–ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD ―Ä–Α–≤–Ϋ–Α 5. –Δ–Ψ―΅–Κ–Α E βÄ™ ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AD. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η AECB.
–ö–Α–Κ–Ψ–Β –Η–Ζ ―¹–Μ–Β–¥―É―é―â–Η―Ö ―É―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Ι –≤–Β―Ä–Ϋ–Ψ?
1) –£―¹–Β ―É–≥–Μ―΄ ―Ä–Ψ–Φ–±–Α ―Ä–Α–≤–Ϋ―΄.
2) –ï―¹–Μ–Η ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Ψ–¥–Ϋ–Ψ–≥–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―Ä–Α–≤–Ϋ―΄ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ –¥―Ä―É–≥–Ψ–≥–Ψ ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―²–Ψ ―²–Α–Κ–Η–Β ―΅–Β―²―΄―Ä―ë―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ―Ä–Α–≤–Ϋ―΄.
3) –ß–Β―Ä–Β–Ζ –Μ―é–±―É―é ―²–Ψ―΅–Κ―É, –Μ–Β–Ε–Α―â―É―é –≤–Ϋ–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Φ–Ψ–Ε–Ϋ–Ψ –Ω―Ä–Ψ–≤–Β―¹―²–Η –¥–≤–Β –Κ–Α―¹–Α―²–Β–Μ―¨–Ϋ―΄–Β –Κ ―ç―²–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η.





–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: