В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
По
определению косинуса cosA=AC/AB => AB=AC/cosA=9/0,3=30.
Ответ: AB=30.
Поделитесь решением
Присоединяйтесь к нам...
Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
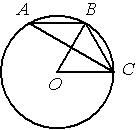Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: