
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ891 –Η–Ζ 1087 |
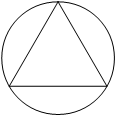
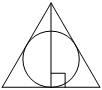 –†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Η–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ, ―Ä–Α–≤–Β–Ϋ 5. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Η–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ, ―Ä–Α–≤–Β–Ϋ 5. –ù–Α–Ι–¥–Η―²–Β –≤―΄―¹–Ψ―²―É ―ç―²–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α.
–ü–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α:
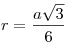
–Δ–Ψ–≥–¥–Α:
6r=a√
a=6r/√
–ü–Ψ –≤―²–Ψ―Ä–Ψ–Φ―É ―¹–≤–Ψ–Ι―¹―²–≤―É
―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α
–≤―΄―¹–Ψ―²–Α ―²–Α–Κ –Ε–Β ―è–≤–Μ―è–Β―²―¹―è –Η
–Φ–Β–¥–Η–Α–Ϋ–Ψ–Ι.
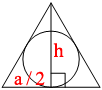 –Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Ψ–Ϋ–Α –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä―É―é –Ψ–Ω–Η―Ä–Α–Β―²―¹―è, –Ω–Ψ–Ω–Ψ–Μ–Α–Φ.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Ψ–Ϋ–Α –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É, –Ϋ–Α –Κ–Ψ―²–Ψ―Ä―É―é –Ψ–Ω–Η―Ä–Α–Β―²―¹―è, –Ω–Ψ–Ω–Ψ–Μ–Α–Φ.
–ö ―²–Ψ–Φ―É –Ε–Β –≤―΄―¹–Ψ―²–Α –Ψ–±―Ä–Α–Ζ―É–Β―²
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Φ–Ψ–Ε–Ϋ–Ψ –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨―¹―è
―²–Β–Ψ―Ä–Β–Φ–Ψ–Ι –ü–Η―³–Α–≥–Ψ―Ä–Α:
a2=h2+(a/2)2
(10√
100*3=h2+(5√
300=h2+25*3
h2=300-75=225
h=√
–û―²–≤–Β―²: 15
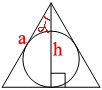 –€–Ψ–Ε–Ϋ–Ψ –≤–Φ–Β―¹―²–Ψ ―²–Β–Ψ―Ä–Β–Φ―΄ –ü–Η―³–Α–≥–Ψ―Ä–Α –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨―¹―è –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–Φ:
–€–Ψ–Ε–Ϋ–Ψ –≤–Φ–Β―¹―²–Ψ ―²–Β–Ψ―Ä–Β–Φ―΄ –ü–Η―³–Α–≥–Ψ―Ä–Α –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨―¹―è –Κ–Ψ―¹–Η–Ϋ―É―¹–Ψ–Φ:–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―Ä–Α–≤–Β–Ϋ 2√
–†–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―Ä–Α–≤–Β–Ϋ 2√
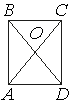 –î–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η AC –Η BD –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABCD –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è
–≤ ―²–Ψ―΅–Κ–Β O, BO=37, AB=56. –ù–Α–Ι–¥–Η―²–Β AC.
–î–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η AC –Η BD –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABCD –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è
–≤ ―²–Ψ―΅–Κ–Β O, BO=37, AB=56. –ù–Α–Ι–¥–Η―²–Β AC.
 –ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α CM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AM=12 –Η MB=18. –ö–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É C, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ω―Ä―è–Φ―É―é AB –≤ ―²–Ψ―΅–Κ–Β D. –ù–Α–Ι–¥–Η―²–Β CD.
–ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α CM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AM=12 –Η MB=18. –ö–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É C, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ω―Ä―è–Φ―É―é AB –≤ ―²–Ψ―΅–Κ–Β D. –ù–Α–Ι–¥–Η―²–Β CD.
 –ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α CM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AM=11 –Η MB=16. –ö–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É C, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ω―Ä―è–Φ―É―é AB –≤ ―²–Ψ―΅–Κ–Β D. –ù–Α–Ι–¥–Η―²–Β CD.
–ë–Η―¹―¹–Β–Κ―²―Ä–Η―¹–Α CM ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC –¥–Β–Μ–Η―² ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB –Ϋ–Α –Ψ―²―Ä–Β–Ζ–Κ–Η AM=11 –Η MB=16. –ö–Α―¹–Α―²–Β–Μ―¨–Ϋ–Α―è –Κ –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Α―è ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É C, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ω―Ä―è–Φ―É―é AB –≤ ―²–Ψ―΅–Κ–Β D. –ù–Α–Ι–¥–Η―²–Β CD.
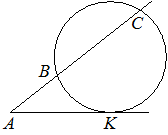 –ß–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É A, –Μ–Β–Ε–Α―â―É―é –≤–Ϋ–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Ω―Ä―è–Φ―΄–Β. –û–¥–Ϋ–Α –Ω―Ä―è–Φ–Α―è –Κ–Α―¹–Α–Β―²―¹―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –≤ ―²–Ψ―΅–Κ–Β K. –î―Ä―É–≥–Α―è –Ω―Ä―è–Φ–Α―è –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨
–≤ ―²–Ψ―΅–Κ–Α―Ö B –Η C, –Ω―Ä–Η―΅―ë–Φ AB=4, BC=32. –ù–Α–Ι–¥–Η―²–Β AK.
–ß–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É A, –Μ–Β–Ε–Α―â―É―é –≤–Ϋ–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ―΄ –¥–≤–Β –Ω―Ä―è–Φ―΄–Β. –û–¥–Ϋ–Α –Ω―Ä―è–Φ–Α―è –Κ–Α―¹–Α–Β―²―¹―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –≤ ―²–Ψ―΅–Κ–Β K. –î―Ä―É–≥–Α―è –Ω―Ä―è–Φ–Α―è –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨
–≤ ―²–Ψ―΅–Κ–Α―Ö B –Η C, –Ω―Ä–Η―΅―ë–Φ AB=4, BC=32. –ù–Α–Ι–¥–Η―²–Β AK.



–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η: