Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
Вариант №1 (прислал Всеволод).
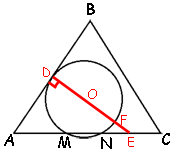Проведем отрезок от точки касания стороны AB и окружности через центр окружности к стороне AC. Обозначим точки как показано на рисунке.
AD2=AM*AN (по
теореме о касательно и секущей для точки А).
AD2=9*11=99
AD=√
Рассмотрим треугольник ADE.
Данный треугольник
прямоугольный (по
свойству касательной).
cos∠BAC=AD/AE (по
определению).
AE=AD/cos∠BAC=3√
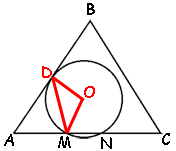Дополнительно обозначим ключевые точки и проведем отрезки, как показано на рисунке.
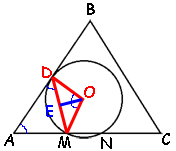По
четвертому свойству углов, связанных с окружностью ∠ADM равен половине градусной меры дуги DM.Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Сторона равностороннего треугольника равна 10√
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Площадь прямоугольного треугольника равна 882√
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-03 21:11:28) Администратор: Василина, cos∠DOE=cos∠BAC, так как ∠DOE=∠BAC. В решении это показано.
(2017-05-02 22:31:56) Администратор: Анатолий, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-05-01 12:54:15) анатолий: в основании пирамиды лежит квадрат.одна из боковых граней перпендикулярна ее основанию а две соседние с ней грани образуют с основанием двугранные углы по 30.найти площадь поверхности пирамиды если ее высота равна h
(2017-04-18 14:36:53) Генрих: Пару дней назад все выслал)
(2017-04-13 12:28:20) Генрих: Все красиво перепишу и постараюсь сегодня выслать)
(2017-04-03 12:06:06) Администратор: Генрих, здравствуйте! Присылайте на admin@otvet-gotov.ru, будем очень благодарны!
(2017-04-03 12:04:55) Администратор: Генрих, здравствуйте! Присылайте на admin@otvet-gotov.ru, будем очень благодарны!
(2017-04-03 03:39:16) Генрих: Здравствуйте, хотел бы поделиться другим решением, куда его можно прислать, мне кажется, оно более универсально.
(2016-02-09 00:51:04) Администратор: Ксения, да, Вы правы, я подумаю, над этим вопросом...Спасибо за информацию.
(2016-02-09 00:41:58) Ксения: опечатка в моем комментарии: косинус=(корень из 15, деленный на 4(!)
(2016-02-09 00:37:24) Ксения: Решала аналогичную задачу с другими цифрами (расстояния 12 и 45 соответственно, косинус=(корень из 15, деленный на 2) первым способом. Получилось, что АЕ=24, что противоречит условию, т.к. АЕ должно быть больше, чем 45... Получается, что решение подходит не для всех задач..
(2015-05-26 17:22:14) Денис: моя задача на пробном ОГЭ (ГИА) в этом году.. аж до сих пор её помню)
(2015-05-05 09:53:28) Администратор: Галина, Вы меня запутали ))) Все нормально в этом варианте. Посмотрите свой же комментарий "АЕ=18, при этом по условию AM=9, AN=11, т.е. AN=20", у Вас AN то равняется 11, то 20...По условию AN=11, значит AE больше, чем AN...
(2015-05-05 09:49:56) Администратор: Галина, да, интересное замечание, я как-то даже не обратил внимания...Спасибо, я подумаю над этим вопросом...
(2015-05-05 09:11:30) Галина: Для варианта №1 АЕ=18, при этом по условию AM=9, AN=11, т.е. AN=20. Т.е. вторая часть решения EN*EM=EF*DE теряет смысл.