В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Площадь
трапеции равна h*(a+b)/2, где a и b - основания трапеции, h - высота трапеции.
hтр*(3+1)/2=12 (по условию задачи)
h=12/2=6
Проведем
высоту треугольника ABC, как показано на рисунке.
hтреугольника=hтр, так как они обе перпендикулярны одним и тем же параллельным основаниям трапеции и образуют прямоугольник.
Sтреугольника=hтреугольника*BC/2=6*1/2=3
Ответ: Sтреугольника=3
Поделитесь решением
Присоединяйтесь к нам...
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Площадь прямоугольного треугольника равна 882√
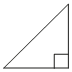В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
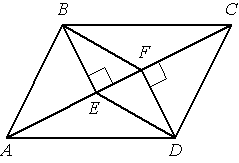В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: