В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-30°-50°=100°.
/ABD=/B/2=50° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=50°+90°+/CBH => /CBH=40°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=100°-50°-40°=10°.
Ответ: /DBH=10°
Поделитесь решением
Присоединяйтесь к нам...
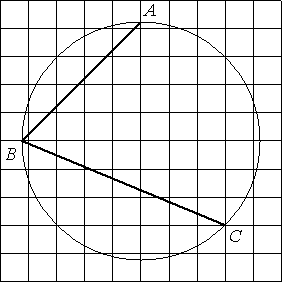Найдите угол ABC. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, высота фонаря 9 м?
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: