Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Рассмотрим каждое утверждение.
1) "
Биссектриса
равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию", это утверждение верно, по
свойству равнобедренного треугольника - такая
биссектриса является и медианой, и высотой, следовательно, она перпендикулярна основанию.
2) "Диагонали
ромба точкой пересечения делятся пополам", это утверждение верно, т.к. это утверждение является
свойством параллелограмма, а
ромб - это тоже
параллелограмм.
3) "Из двух хорд окружности больше та, середина которой находится дальше от центра окружности", это утверждение неверно. Диаметр - это наибольшая
хорда, следовательно, чем центр хорды ближе к центру окружности, тем хорда больше.
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен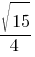 
. Найдите CosA.
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
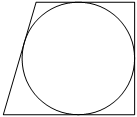Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: