В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-20°-60°=100°.
/ABD=/B/2=50° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=60°+90°+/CBH => /CBH=30°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=100°-50°-30°=20°.
Ответ: /DBH=20°
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 968√
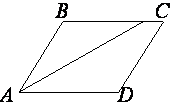Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
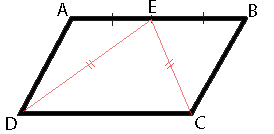В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30Х40Х50 (см) можно поместить в кузов машины размером 3Х2Х3,5 (м)?
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 21°?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-03-13 23:54:51) Администратор: Спасибо за найденную опечатку, исправлено.
(2016-03-12 14:31:32) : Исправьте, пожалуйста, в ответе угол СВН на DBH.