
 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
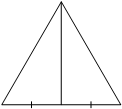
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
 Введем обозначения как показано на рисунке.
Введем обозначения как показано на рисунке.
По
определению равностороннего треугольника:
AB=BC=AC=14√3
По
свойству равностороннего треугольника, медиана является так же и
биссектрисой, и
высотой.
Следовательно:
1) BD перпендикулярен AC (т.к. BD -
высота), т.е. треугольник ABD -
прямоугольный.
2) AD=AC/2 (т.к. AC - медиана).
По
теореме Пифагора:
AB2=BD2+AD2
AB2=BD2+(AC/2)2
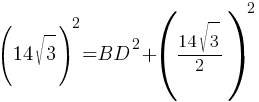
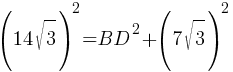
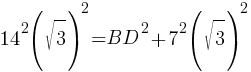
196*3=BD2+49*3
588=BD2+147
BD2=588-147=441
BD=√441=21
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
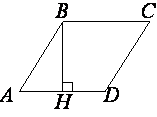 Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
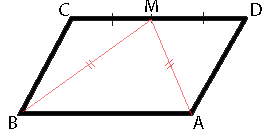 В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.



Комментарии: