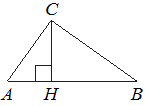
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Рассмотрим треугольники ACH и BCH.
Докажем, что это подобные треугольники:
∠AHC=∠BHC=90° (так как CH -
высота).
По
теореме о сумме углов треугольника:
180°=∠CAH+∠AHC+∠HCA
180°=∠CAH+90°+∠HCA
90°=∠CAH+∠HCA
∠CAH=90°-∠HCA
Заметим, что:
∠BCH=90°-∠HCA
Получается, что ∠CAH=∠BCH
Тогда, по первому признаку подобия, данные треугольники подобны, т.е. можем записать пропорцию:
AH/CH=CH/BH
AH*BH=CH2
2*18=CH2
36=CH2
CH=√36=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-02-28 13:41:15) Юля: Прямая параллельная стороне АС треугольника АВС , пересекает стороны АВ и ВС в точках М и N соответственно. АВ =8 , АС =8 , МN= 2 Найдите АМ