В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=35°+58°=93°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, ∠BAD=∠ADC=93°.
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ABD+∠BDA
180°=93°+∠ABD+35°
∠ABD=180°-93°-35°
∠ABD=52°
Ответ: 52
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 512√
В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
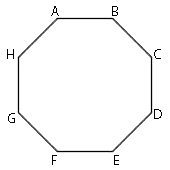ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: