В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Обозначим точку пересечения диагоналей как О.
По
свойству
параллелограмма AO=OC=AC/2.
AB=CD (по
другому свойству).
А так как AC в 2 раза больше стороны AB (по условию задачи), то OC=AB=CD.
Следовательно треугольник OCD -
равнобедренный.
По
свойству равнобедренного треугольника /COD=/CDO.
По
теореме о сумме углов треугольника:
180°=∠COD+∠CDO+∠ACD=∠COD+CDO+1°
∠COD+∠CDO=179°, а так как ∠COD=∠CDO (это мы выяснили ранее), то ∠COD=∠CDO=179°/2=89,5°
Второй угол между диагоналями:
∠BOC=180°-∠COD (т.к. угол BOD - развернутый и равен 180°)
∠BOC=180°-89,5°=90,5°
Ответ: ∠COD=89,5°, ∠BOC=90,5°
Поделитесь решением
Присоединяйтесь к нам...
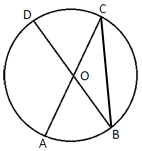В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
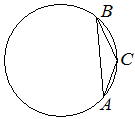В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-16 20:21:28) Светлана: За угол между двумя пересекающимися прямыми принято принимать меньший.Так что ответ определяется однозначно.
(2015-05-11 20:27:58) Администратор: По логике да, два ответа, но как лучше писать на экзамене, уточните у своего педагога по математике.
(2015-05-11 17:25:44) : Здесь получается два ответа?