
 Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
 Проведем отрезок CO.
Проведем отрезок CO.
Рассмотрим треугольник ACO.
∠ACO=∠ACB/2=76°/2=38° (по
второму свойству касательной).
∠CAO=90° (по
первому свойству касательной)
По
теореме о сумме углов треугольника:
180°=∠AOC+∠ACO+∠CAO
180°=∠AOC+38°+90°
∠AOC=52°
Рассмотрим треугольники ACO и BCO.
OC - общая сторона
AC=BC (по
второму свойству касательной)
OA=OB (т.к. это радиусы)
Следовательно, по
третьему признаку, данные треугольники равны.
Тогда и ∠AOC=∠BOC=52°
Рассмотрим треугольник AOB.
OA=OB (т.к. это радиусы)
Следовательно, треугольник AOB -
равнобедренный.
Тогда ∠BAO=∠ABO (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OAB+∠ABO
180°=∠AOC+∠BOC+2∠ABO
180°=52°+52°+2∠ABO
76°=2∠ABO
∠ABO=38°
Ответ: 38
Поделитесь решением
Присоединяйтесь к нам...
 Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
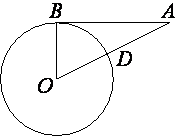 Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
 В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
 Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
 Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
Комментарии:
(2017-04-17 02:23:55) Администратор: Максим, решите свою задачу аналогично этой.
(2017-04-15 12:00:05) Максим: Касательные A и B окружности с центром O пересекаются под углом 38 градусов. Найдите угол ABO. Ответ дайте в градусах.
(2016-10-22 20:21:22) Администратор: варя, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-21 19:36:00) варя: На какой(в градусах)поворачивается минут на стрелка,пока часовая проходит 24