Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Т.к. AC является диаметром, значит треугольник ABC - прямоугольный с гипотенузой AC и ∠B=90° (по
теореме об описанной окружности).
Тогда по теореме сумме углов треугольника:
180°=∠A+∠B+∠C
180°=83°+90°+∠C
∠C=180°-83°-90°
∠C=7°
Ответ: ∠C=7°
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
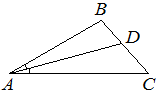В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=36, BC=42 и CD=24.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-23 11:18:15) Администратор: Лена, я поправил решение, конечно использовалась не теорема Пифагора, а теорема о сумме углов треугольника.
(2015-05-23 05:42:52) Лена: и 90 ?
(2015-05-23 05:40:42) Лена: откуда 180 градусов?