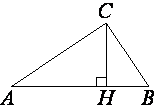
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-20°-50°=110°.
/ABD=/B/2=55° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=50°+90°+/CBH => /CBH=40°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=110°-55°-40°=15°.
Ответ: /DBH=15°
Поделитесь решением
Присоединяйтесь к нам...
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
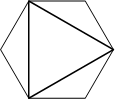Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 14°?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: