В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-20°-60°=100°.
/ABD=/B/2=50° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=60°+90°+/CBH => /CBH=30°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=100°-50°-30°=20°.
Ответ: /DBH=20°
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
Синус острого угла A треугольника ABC равен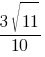 
. Найдите CosA.
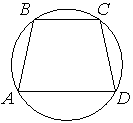Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Площадь равнобедренного треугольника равна 196√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-03-13 23:54:51) Администратор: Спасибо за найденную опечатку, исправлено.
(2016-03-12 14:31:32) : Исправьте, пожалуйста, в ответе угол СВН на DBH.