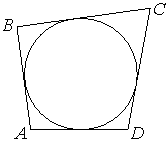
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
По
свойству вписанной в четырехугольник окружности:
AD+BC=AB+CD
AD+13=9+18
AD=9+18-13=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен 
. Найдите CosA.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: