
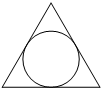
 Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
По
четвертому свойству равностороннего треугольника:
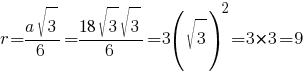
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Синус острого угла A треугольника ABC равен 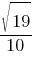 . Найдите CosA.
. Найдите CosA.
 В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
 Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
Комментарии: