
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
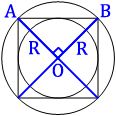 Проведем диаметры
описанной окружности, как показано на первом рисунке.
Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(38√
AB2=2*382*2
AB2=382*22=(38*2)2=762
AB=76
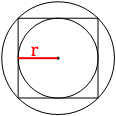 Проведем радиус
вписанной окружности, как на втором рисунке.
Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=76/2=38
Ответ: 38
Поделитесь решением
Присоединяйтесь к нам...
 Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
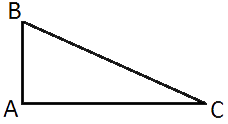 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
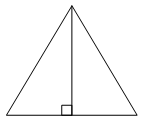 Высота равностороннего треугольника равна 15√
Высота равностороннего треугольника равна 15√
Комментарии: