Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Обозначим как "х" процентное содержание кислоты в первом растворе.
Обозначим как "y" процентное содержание кислоты во втором растворе.
Напомним, что 1 процент (%) от числа - это 0,01 от этого числа.
Получаем уравнение из условия 1 (Если их слить вместе, то получим раствор, содержащий 55% кислоты):
10x+16y=(10+16)*0,55
10x+16y=26*0,55
10x+16y=14,3
Получаем уравнение из условия 2 (Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты), для удобства возьмем по одному кг каждого раствора:
1*x+1*y=(1+1)*0,61
x+y=2*0,61
x+y=1,22
Получили систему уравнений:
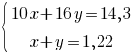
Умножим второе уравнение на 10:
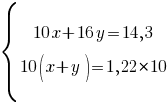
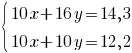
А теперь, чтобы избавиться от "х", вычтем из первого уравнения второе:
(10x+16y)-(10x+10y)=14,3-12,2
10x+16y-10x-10y=2,1
6y=2,1
y=0,35 - это концентрация кислоты во втором растворе.
Подставим полученное значение "y" во второе уравнение и найдем "x":
x+0,35=1,22
x=1,22-0,35=0,87
Найдем, сколько килограммов кислоты содержится в первом растворе:
10*0,87=8,7
Ответ: 8,7
Поделитесь решением
Присоединяйтесь к нам...
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
Стороны AC, AB, BC треугольника ABC равны 3√
В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: