Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
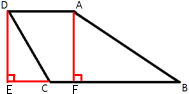Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-120°=60° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin60°=ED/CD (sin60°=√3/2 по
таблице)
√3/2=ED/34
ED=34√3/2
sin(∠ABF)=AF/AB (по
определению)
sin45°=ED/AB
AB=ED/sin45° (sin45°=√2/2 по
таблице)
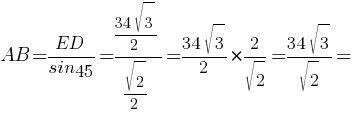
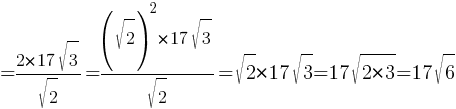
Ответ: 17√6
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности, описанной около квадрата, равен 14√
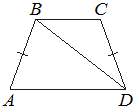В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: