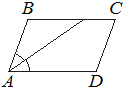
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
AD||BC (по определению параллелограмма).
Тогда биссектрису можно рассматривать как секущую.
∠BCA=∠DAC=41° (так как это накрест лежащие углы).
∠DAC=∠BAC=41° (по определению биссектрисы).
∠BAD=∠BAC+∠DAC=41°+41°=82°
Ответ: 82
Поделитесь решением
Присоединяйтесь к нам...
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
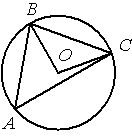Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-03-06 09:48:37) : Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 40°. Ответ дайте в градусах.