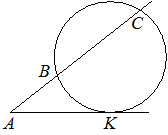
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
По
теореме о касательной и секущей:
AK2=AB*AC
AK2=AB*(AB+BC)
AK2=8*(8+24)=256
AK=√256=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: