
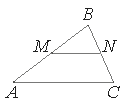
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
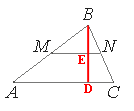 Проведем
высоту BD из вершины B.
Проведем
высоту BD из вершины B.
Площадь треугольника ABC:
SABC=BD*AC/2
162=BD*36/2
BD=162*2/36=9
Рассмотрим треугольники ABC и MBN.
∠B - общий.
∠BAC=∠BMN (так как это
соответственные углы).
Следовательно, данные треугольники
подобны (по двум углам).
Тогда, справедливо соотношение сторон и высот данных треугольников:
AC/MN=BD/BE
BE=MN*BD/AC=28*9/36=28/4=7
Площадь треугольника ABC:
SMBN=BE*MN/2=7*28/2=7*14=98
Ответ: 98
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB=9.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB=9.
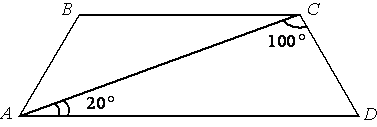 Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Комментарии:
(2019-01-19 12:02:26) Администратор: Алина, это условие задачи.
(2019-01-10 13:30:34) алина: как получилось 162?
(2017-05-14 18:51:30) Администратор: Людмила, а про отношение площадей подобных треугольников говорится в каком-нибудь учебнике?
(2017-05-13 18:42:00) Людмила: Можно короче: отношение площадей подобных треугольников равно коэффициенту подобия в квадрате. К=28/36 = 7/9, значит отношение площадей треугольников = 49/81 Тогда S = 162*(49/81) = 98