
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
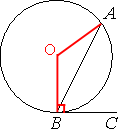 Проведем отрезки из центра окружности к точкам А и В, как показано на рисунке.
Проведем отрезки из центра окружности к точкам А и В, как показано на рисунке.
∠AOB - центральный, следовательно равен градусной мере дуги, т.е. ∠AOB=92°.
Рассмотрим треугольник OAB:
OA=OB, так как это радиусы окружности.
Получается, что данный треугольник
равнобедренный.
Следовательно, ∠OAB=∠OBA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OAB+∠OBA
180°=92°+x+x
2x=88°
x=44°
∠OBC=90° (по
свойству касательной).
∠ABC=∠OBC-∠OBA
∠ABC=90°-44°
∠ABC=46°
Ответ: 46
Поделитесь решением
Присоединяйтесь к нам...
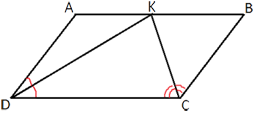 Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
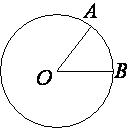 На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ∠AOB=40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги.
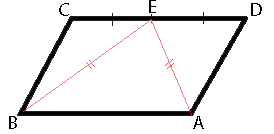 В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
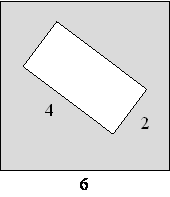 Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
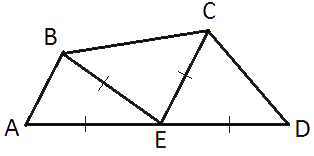 Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Комментарии:
(2019-10-09 20:18:09) Администратор: meltdown, как?
(2019-10-09 20:09:23) meltdown: помогите пожалуйста
(2017-05-14 18:59:05) Администратор: Людмила, в математике утверждений не бывает. Бывают определения, теоремы и аксиомы. Поэтому при решении или надо ссылаться на определения, теоремы и аксиомы, или доказывать.
(2017-05-13 18:50:59) Людмила: Можно просто воспользоваться утверждением, что угол между хордой и касательной равен половине дуги, заключенной внутри него. Доказывать это не обязательно