
 Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Рассмотрим треугольник ALD.
AL вдвое меньше AB (по условию задачи).
AD тоже вдвое меньше AB (по условию задачи), следовательно:
AL=AD
Т.е. данный треугольник
равнобедренный.
По
свойству равнобедренного треугольника ∠ADL=∠ALD
∠ALD=∠LDC (т.к. это
накрест-лежащие углы).
Получается, что ∠ADL=∠LDC.
Следовательно DL -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
 Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
 В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
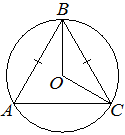 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Комментарии: