Синус острого угла A треугольника ABC равен √
Вариант №1
В условии задачи про треугольник ничего не сказано. Но мы можем нарисовать такой прямоугольный треугольник, чтобы и у него
синус острого угла был равен √
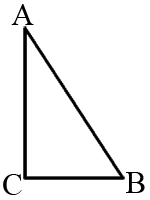Чтобы sinA был равен √
По тоереме Пифагора:
AB2=CB2+AC2
52=(√
25=21+AC2
AC2=4
AC=2
Тогда, по определению
косинуса:
cosA=AC/AB=2/5=0,4
Ответ: 0,4
Вариант №2
Воспользуется
основной тригонометрической формулой:
sin2A+cos2A=1
(√
21/25+cos2A=1
cos2A=1-21/25=1-0,84=0,16
cosA=0,4
Ответ: 0,4
Поделитесь решением
Присоединяйтесь к нам...
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
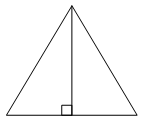Высота равностороннего треугольника равна 15√
На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: