
Прямая y=2x+b касается окружности x2+y2=5 в точке с положительной абсциссой. Определите координаты точки касания.
Чтобы определить точку касания двух графиков, необходимо решить систему, составленную их функций этих графиков:
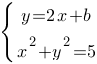
Подставим первое уравнение во второе:
x2+(2x+b)2=5
Раскроем скобку при помощи формулы
квадрат суммы:
x2+(2x)2+2*2x*b+b2=5
x2+4x2+4xb+b2=5
5x2+4xb+b2-5=0
Решим это квадратное уравнение через дискриминант:
D=(4b)2-4*5*(b2-5)=16b2-20(b2-5)=16b2-20b2+100=-4b2+100
В условии сказано, что прямая КАСАЕТСЯ окружности, следовательно имеет только одну общую точку, следовательно, решение системы должно быть только одно, т.е. решение
квадратного уравнения тоже должно быть одно. Для этого
дискриминант должен быть равен нулю:
-4b2+100=0
-4b2=-100 |:(-4)
b2=25
b1=5
b2=-5
Мы получили такие b, при которых прямая y=2x+b будет иметь только одну общую точку (т.е. касаться) с окружностью x2+y2=5.
Продолжим решать квадратное уравнение для каждого b:
1) b=5
Тогда наше уравнение имеет вид:
5x2+4x*5+52-5=0
5x2+20x+25-5=0
5x2+20x+20=0 |:5
x2+4x+4=0
Дискриминант равен нулю, мы его сами приравняли к нулю. Найдем x:
x=-4/(2*1)=-4/2=-2 - это абцисса точки пересечения, она отрицательна, поэтому не подходит по условию задачи.
2) b=-5
Тогда наше уравнение имеет вид:
5x2+4x(-5)+(-5)2-5=0
5x2-20x+25-5=0
5x2-20x+20=0 |:5
x2-4x+4=0
x=-(-4)/2=4/2=2 - эта абцисса подходит под условие.
Подставим эти значения х и b в уравнение прямой:
y=2x+b
y=2*2-5
y=-1 - это ордината точки пересечения.
Ответ: (2;-1)
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
Комментарии: