
 В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
NK - является
средней линией треугольника ABC и равна половине AB.
MK - является
средней линией треугольника ABC и равна половине BC.
Т.к. AB=BC (по условию), то NK=MK.
Следовательно треугольник MNK -
равнобедренный.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 8√
Площадь прямоугольного треугольника равна 8√
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
 Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
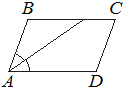 Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Комментарии: