
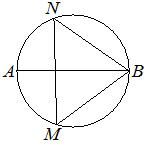
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
∠NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 36°*2=72°.
Тогда дуга NB равна 180°-72°=108°
∠NMB - тоже является
вписанным в окружность и опирается на дугу NB, следовательно он равен 108°/2=54°
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
Укажите номера верных утверждений.
1) Диагонали любого прямоугольника равны.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
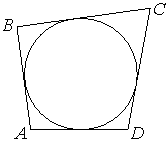 Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Комментарии: