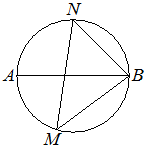
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
∠NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 41°*2=82°.
Тогда дуга NB равна 180°-82°=98°
∠NMB - тоже является
вписанным в окружность и опирается на дугу NB, следовательно он равен 98°/2=49°
Ответ: 49
Поделитесь решением
Присоединяйтесь к нам...
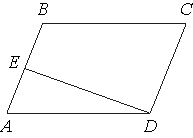В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 80°. Найдите величину угла ODC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K,
длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Найдите тангенс угла AOB, изображённого
на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: